Algorithms and Problem Solving
A curated list of fundamental questions and answers for Unit 03.
1. Differentiate between well-defined and ill-defined problems within the realm of computational problem-solving.
Problems can be categorized based on how clearly they are defined:
- Well-defined Problems: These problems have clear goals, inputs, processes, and outputs. For instance, the problem of determining if a number is even is a well-defined problem because it has a clear goal, clear input (a single integer), a clear process (check if the number is divisible by 2), and a clear output (even or odd).
- Ill-defined Problems: These problems lack clear definitions or may have ambiguous goals and requirements. For instance, consider a project aimed at “improving education in Pakistan”. This goal is vague and broad, and it’s not clear what inputs are available or what a successful output would look like.
2. Outline the main steps involved in the Generate and Test algorithm.
The Generate and Test algorithm involves two main steps:
- Generate: In this step, the algorithm generates possible solutions to the problem. These solutions can be generated randomly, systematically, or based on some heuristic.
- Test: After generating a potential solution, the algorithm tests it against the problem’s requirements or constraints. If the solution is valid, the process stops. If not, the algorithm generates a new solution and repeats the test.
3. Compare tractable and intractable problems in the context of computational complexity.
- Tractable Problems: A problem is considered tractable if it can be solved in polynomial time (P). This means the time to solve the problem increases at a manageable rate as the input size grows. An example is sorting a list using Merge Sort.
- Intractable Problems: These problems require super-polynomial time to solve, often growing exponentially with the input size. They are impractical to solve for large inputs because the required time becomes unmanageable.
4. Summarize the key idea behind Greedy Algorithms.
Greedy algorithms work by making a sequence of choices that are locally optimal at each step, with the hope that these choices will lead to a globally optimal solution. It does not go back and change decisions once they are made.
5. Discuss the advantages of using Dynamic Programming.
Dynamic Programming (DP) solves problems by breaking them into simpler subproblems and storing the results to avoid redundant calculations. It saves time by using memoization or tabulation and is great for problems with overlapping subproblems, like calculating the Fibonacci sequence.
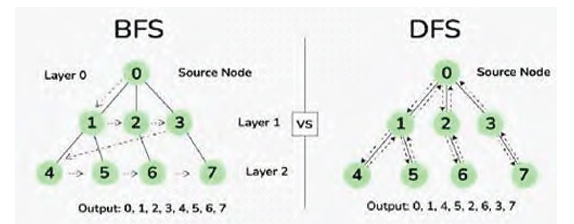
6. Compare the advantages of Breadth-First Search (BFS) with Depth-First Search (DFS) in graph traversal.
Breadth-First Search (BFS)
BFS explores a graph level by level, starting from a given node. It uses a queue and is ideal for finding the shortest path between two nodes.
Depth-First Search (DFS)
DFS explores as far down a branch as possible before backtracking. It uses a stack and is useful for solving puzzles or maze-like problems.
7. Explain the importance of breaking down a problem into smaller components in algorithmic thinking.
- It makes complex problems easier to solve.
- It helps in reusing code (modularity).
- It makes the solution clearer and more organized.
- It is easier to test and debug each individual part.
8. Identify the key factors used to evaluate the performance of an algorithm.
Efficiency
How well an algorithm uses resources like time and space (memory). It’s evaluated by its time complexity (how runtime grows with input size) and space complexity (how memory usage grows).
Scalability
An algorithm’s ability to maintain its efficiency as the size of the input data grows. A scalable algorithm performs well even with very large inputs.
Suitability
Not all algorithms are suitable for all problems. The choice depends on the problem’s specific requirements, such as the need for speed, memory constraints, or the nature of the data.
